

A high-level handling mode of the liftoplane is referenced as biangular handling. The diagram below explains it.
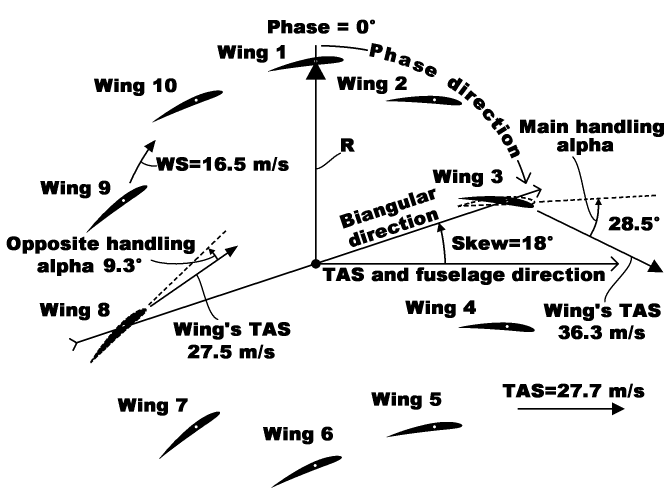
The main idea here: this high-level handling should have a direct relation with angles of attack of the wings at two opposite points in a certain direction. This direction is selected to be pointed by the Skew angle of the PGS-state, and thus it is equal to the gain direction. So, there are two AoAs for the main and opposite points. In aerodynamics AoA is also referred to as angle alpha. And so, I refer to these two angles as the main handling alpha and the opposite handling alpha, and they are reflected in this diagram, which utilizes the same PGS-state as the diagram of explanation of the PGS-state. These two angles are represented for Wing 3 and Wing 8, respectively. The main difference between this handling and the PGS-state is the use of airflow conditions associated with these angles in such a way that these two angles are independent of changes in the parameters of these flow conditions themselves. For example, after providing particular values of the biangular angles to some flight software routine, they will be constant for any change in airspeed and for any change in the winding speed of the rotor. This constant behavior will be ensured by corresponding changes in the P and G components of the PGS-state by using this routine to reflect changes in airspeed and rotor's winding speed. The diagram provides an example of the relationship of the pictured winding speed WS and the true aerodynamic speed TAS of the entire aircraft, which is parallel to the fuselage in this handling mode, with two particular TASs of Wing 3 and Wing 8. The angles of attack relative to these two TAS-vectors imply two related pitches for these two wings. Such positions of the wings and the directions of their chords are depicted in dotted lines on the diagram. And they aren’t equal to the actual pitches performed. This differing feature reflects a special correction of the asymmetry of the pitch variation imposed by the gain to the main and opposite points. This correction matters for high gain values and is close to zero for low gain values. Additionally, if exists some remaining error angle between the fuselage and the TAS-vector, this error angle should be in consideration during handling and should be used to correct the resulting PGS-state.
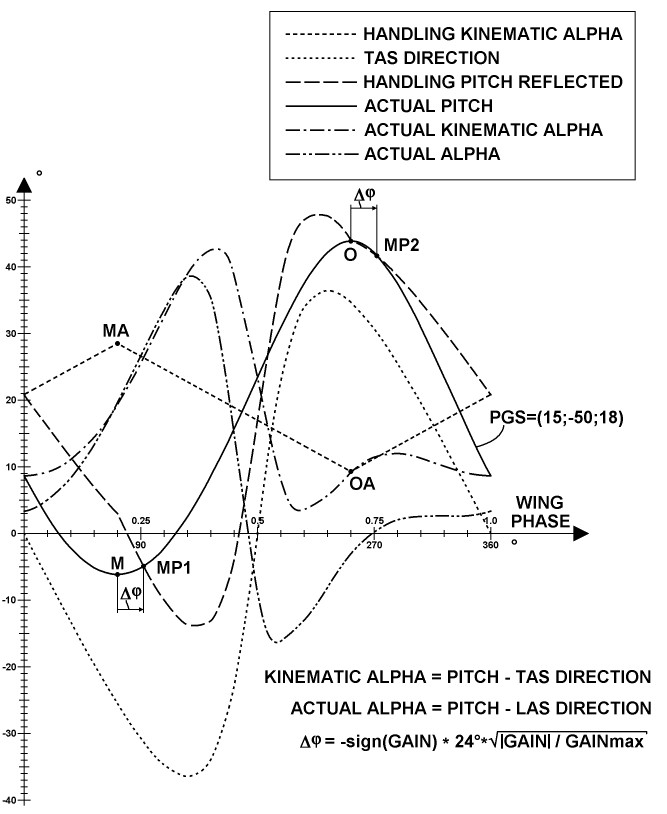
The chart above represents a plot of the distributions of all related angular components involved in the biangular handling over all positions of the rotor wings of the example of the previous diagram. At first, there are values of the HANDLING KINEMATIC ALPHA. The word "kinematic" means that the reference flow is simply the vectorial sum of the TAS of the aircraft and the kinematic speed of a particular wing, for its particular phase. This does not include dynamic perturbations in airflow arising from the actual vorticity distribution over the entire rotor. This exclusion means: any handling parameters must be free of all dynamic components containing uncertainty errors, for a steady referencing. And those biangular values are merely kinematic parameters, although some level of uncertainty can still exist upon measuring the TAS. This primary handling distribution is selected so that it is simply linear between the main alpha (MA) and the opposite alpha (OA). At second, there are values of the TAS DIRECTION itself. At third, there are values of the HANDLING PITCH REFLECTED from the first relation for the kinematic alpha referenced at the bottom of the plot. These last values correspond to the pitches depicted in dotted lines in the previous diagram. Fourth, there are values of the ACTUAL PITCH resulted from the PGS-state. These two kinds of pitch are connected using two match points: MP1, which is shifted from the main direction M of the PGS-state by an angle Δφ, and MP2, which is shifted from the opposite direction O of the PGS-state by the same angle. The formula for the shifting angle is represented in the third equation at the bottom of the plot. It uses the Gain itself and is simply the best approximation for fitting the actual pitch distribution to the desired handling pitch distribution, which I found through numerical experimentation. The flight software routine uses the Gain value from the previous servicing cycle in this equation, since the Gain is also a component of the target result of the fitting these match points. Fifth, there are values of the ACTUAL KINEMATIC ALPHA recovered using the first relation referenced at the bottom of the plot. And sixth, there are values of the ACTUAL ALPHA recovered using the second relation referenced at the bottom of the plot. The second relation uses LAS instead of TAS. To obtain this LAS, the perturbations of the base flow by vorticity were split into the inflow component and the interference distribution component as a result of numerical simulation. And the entire result corrects the TAS to this LAS.
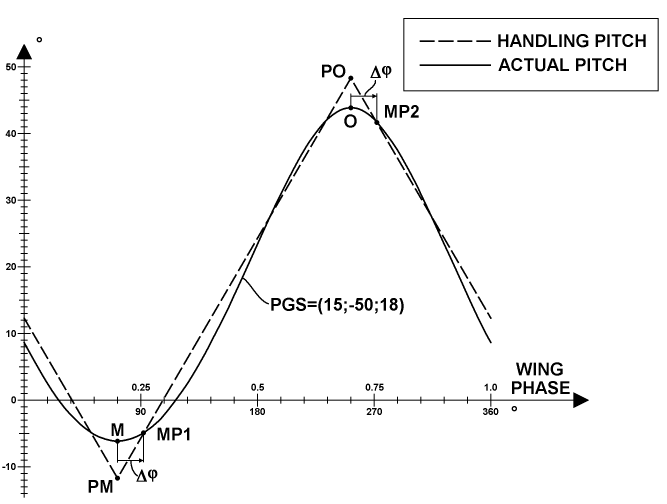
There is also a simplified variant of the biangular handling mode that ignores airflow conditions, for rare use, which I call biangular pitch handling. The chart above represents a plot of pitch distributions over all positions of the rotor wings in this case, utilizing the same PGS-state as for the biangular alpha handling. The ACTUAL PITCH distribution is depicted together with the values of the HANDLING PITCH, which are also selected so that they are simply linear between the main pitch (PM) and the opposite pitch (PO), as for alpha mode. The matching between two kinds of pitches is performed according to the same algorithm as for alpha mode.
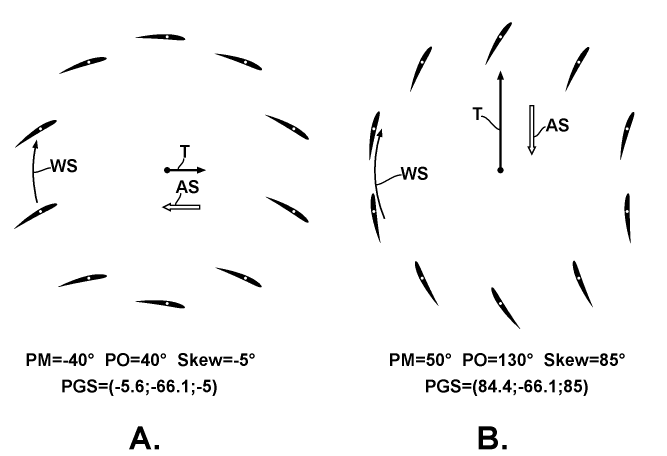
The chart above represents two diagrams designated as A. and B. of the particular use of biangular pitch handling in a such named "propelling" mode upon accelerating on the runway and upon a vertical takeoff attempt, respectively. These diagrams depict the relationship between the wings' pitching, the thrust T, the winding speed WS and the airspeed AS. The main feature of this mode is that the P value of the PGS is almost same as the S value and follows its change. Here, the PM and PO values are used for reference only. The thrust force in the second case is still not enough to accomplish its task. Also, a detailed comparative analysis with an equivalent rotor operated in curtate mode indicates a lower thrust than the rotor presented, but it also has a much lower external moment and consumed power. And if enough power for this takeoff will be provided for both kinds of rotors, the rotor with curtate movement will spend much less power with much lower external moment, but will have the winding speed much higher than that of the presented rotor, so too high centrifugal forces will damage it before this condition is met.
Copyright © 2018-2023 Yuri Feldman - All Rights Reserved